Les réseaux de neurones profonds ont permis des merveilles technologiques allant de la reconnaissance vocale à la transition des machines en passant par l’ingénierie des protéines, mais leur conception et leur mise en œuvre sont néanmoins sans principes. Développer des outils et des méthodes pour guider ce processus est l’un des grands défis de la théorie de l’apprentissage en profondeur. Dans la rétro-ingénierie d’un noyau fantôme neuronal, nous proposons un modèle pour apporter certains principes à l’art de la conception architecturale en utilisant des percées théoriques récentes : commencez par concevoir une bonne fonction du noyau – souvent une tâche beaucoup plus facile – puis “rétroconcevez” le réseau – l’équation du noyau pour traduire le noyau choisi en un réseau de neurones. Notre principal résultat théorique permet de concevoir des fonctions d’activation à partir des premiers principes, et nous l’utilisons pour construire une fonction d’activation qui simule les performances du réseau profond \(\textrm{ReLU }\) avec une seule couche cachée et une autre couche qui surpasse nettement la performance profonde \(\textrm{ReLU }\ ) dans une mission synthétique.
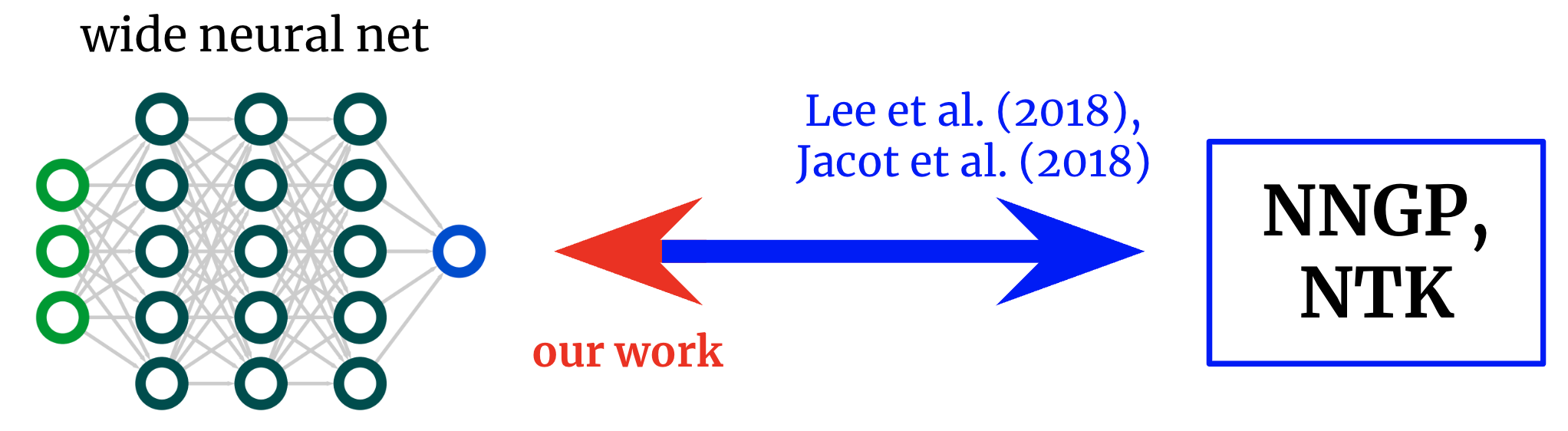
noyau vers les réseaux. Les travaux fondamentaux ont dérivé des formules qui mappent des réseaux de neurones à grande échelle à leurs noyaux correspondants. Nous obtenons un mappage inverse, qui nous permet de partir d’un noyau souhaité et de le ramener à une structure de réseau.
noyau de réseau de neurones
Le domaine de la théorie de l’apprentissage en profondeur a récemment été transformé par la prise de conscience que les réseaux de neurones profonds deviennent souvent susceptibles d’être étudiés en analytique. largeur infinie Limite. Prenez la limite d’une certaine manière, et le réseau converge en fait vers la méthode du noyau normal en utilisant soit un “noyau d’ombre neuronale” (NTK) ou, si seule la dernière couche est formée (similaire aux modèles de caractéristiques aléatoires), un réseau “gaussien”. processus” (NNGP) noyau. Comme le théorème des limites centrales, les limites de grille larges sont souvent des approximations étonnamment bonnes, même loin d’une largeur infinie (souvent vraies lorsque les largeurs se comptent par centaines ou par milliers), ce qui donne un joli contrepoint analytique aux énigmes d’apprentissage en profondeur.
Des réseaux au cœur et vice-versa
Un travail original explorant la correspondance réseau-noyau a donné à ces formules bâtiment pour noyau: Comme l’architecture est décrite (telle que la profondeur et la fonction d’activation), elle vous donne deux cœurs de réseau. Cela a permis de mieux comprendre l’optimisation et la généralisation de divers concepts d’attention. Cependant, si notre objectif n’est pas seulement de comprendre les architectures existantes mais de concevoir nouveau A partir d’eux, on peut préférer tracer les cartes dans le sens inverse : étant donné un noyau Nous voulons, pouvons-nous trouver bâtiment Qui nous le donne ? Dans ce travail, nous dérivons cette cartographie inverse des réseaux entièrement connectés (FCN), nous permettant de concevoir des réseaux simples de manière provisoire en (a) soustrayant un noyau souhaité et (b) en concevant une fonction d’activation qui l’accorde.
Pour voir pourquoi cela a du sens, imaginons d’abord NTK. Considérons un NTK large pour FCN \(K (x_1, x_2)\) sur deux vecteurs d’entrée \(x_1\) et \(x_2\) (que nous supposerons par souci de simplicité est normalisé à la même longueur). Pour FCN, ce noyau est rotation fixe Autrement dit, K (x_1, x_2) = K(c), où c est le cosinus de l’angle entre les entrées. Puisque K (c) est une fonction scalaire de l’argument scalaire, nous pouvons simplement le tracer. La figure 2 montre le NTK d’un FCN à quatre couches cachées (4HL) \(\textrm{ReLU}\).
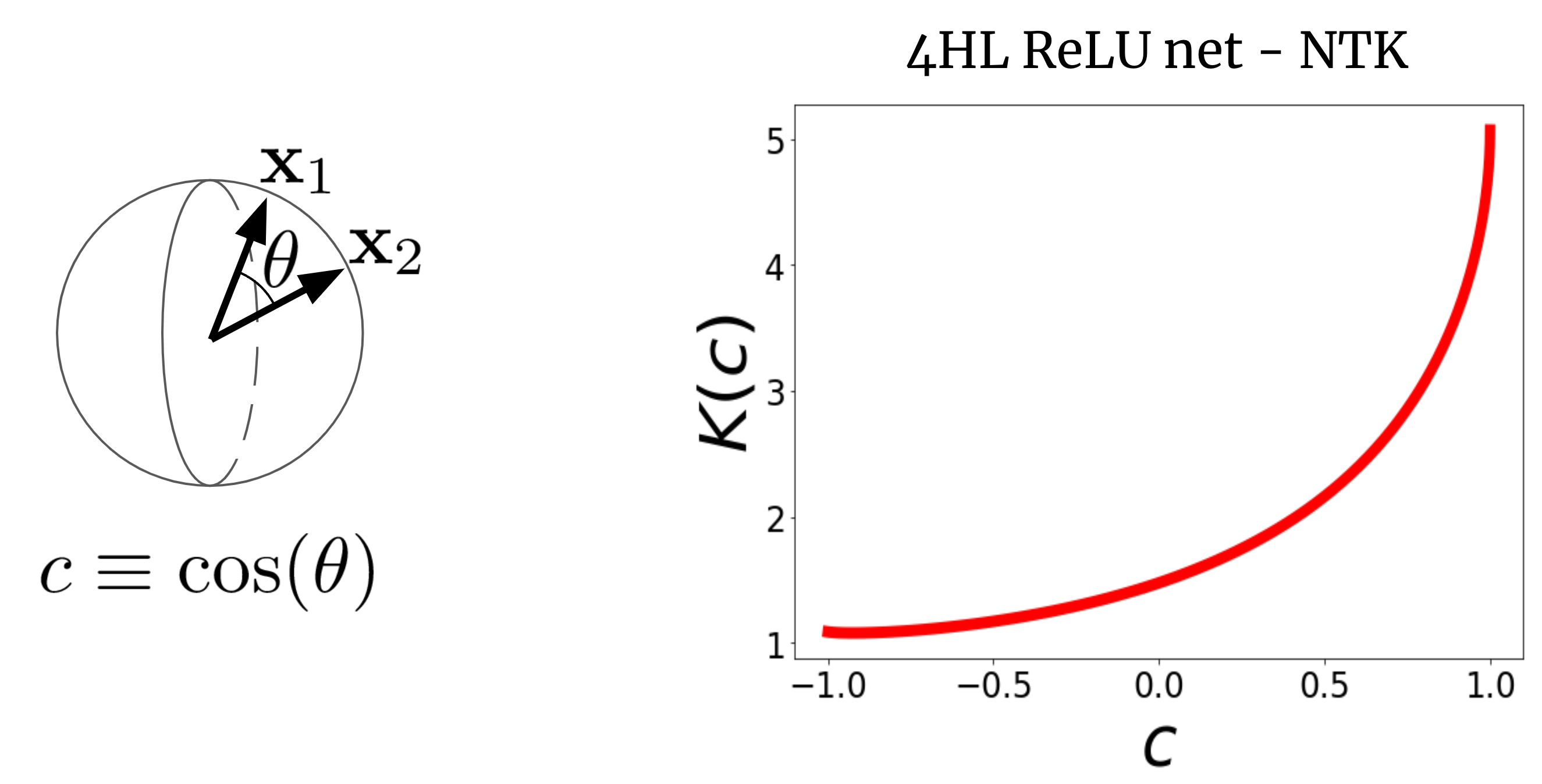
photo 2. NTK pour 4HL ReLU FCN en fonction du cosinus entre les vecteurs d’entrée x1 et x2.
Ce graphique contient en fait beaucoup d’informations sur le comportement d’apprentissage du WAN correspondant ! L’augmentation monotone signifie que ce noyau s’attend à ce que des points plus proches aient des valeurs de fonction plus corrélées. La forte augmentation à la fin nous indique que la longueur du lien n’est pas trop grande et qu’elle peut s’adapter à des fonctions complexes. La dérivée bifurquée en c = 1 nous indique la régularité de la fonction que nous espérons obtenir. Plus important , Aucun de ces faits n’émerge lorsque l’on regarde un tracé \(\textrm{ReLU}(z)\)! Nous affirmons que si nous voulons comprendre l’effet du choix de la fonction d’activation \(\phi \), le NTK résultant est en fait plus informatif que \(\phi \) lui-même. Alors peut-être qu’il est plus logique d’essayer de modéliser les architectures dans “l’espace du noyau”, puis de les traduire en hyper-paramètres typiques.
fonction d’activation pour chaque noyau
Notre résultat principal est la “théorie de l’ingénierie inverse” qui stipule :
Eux 1 : Pour tout noyau K(c), on peut créer une fonction d’activation tildephi telle que, insérée dans Une couche cachée Le noyau FCN, NTK ou NNGP de largeur infinie est K(c).
Nous introduisons une formule explicite pour \tilde {\phi } en termes de polynômes d’Hermite (bien que nous utilisions une formule fonctionnelle différente dans la pratique pour des raisons d’apprentissage). Notre utilisation proposée de ce résultat est que, dans des problèmes avec certaines architectures connues, il sera parfois possible d’écrire et de désosser un bon noyau dans un réseau entraînable avec divers avantages par rapport à la régression du noyau pur, tels que l’efficacité de calcul et la capacité d’apprendre caractéristiques. Comme preuve de concept, nous testons cette idée sur la composition problème de parité (c’est-à-dire étant donné une chaîne de bits, la somme est-elle paire ou impaire ?), ce qui crée immédiatement une fonction d’activation qui surpasse largement \text{ReLU} dans la tâche.
Une couche cachée est tout ce dont vous avez besoin ?
Voici une autre utilisation surprenante de notre découverte. La courbe de noyau ci-dessus est pour 4HL\(\textrm{ReLU}\)FCN, mais j’ai affirmé que nous pouvons réaliser n’importe quel noyau, y compris ceux-ci, avec une seule couche cachée. Cela signifie que nous pouvons proposer de nouvelles fonctions d’activation \(\tilde {\phi }\) qui donnent le NTK “profond” dans réseau peu profond! La figure 3 illustre cette expérience.
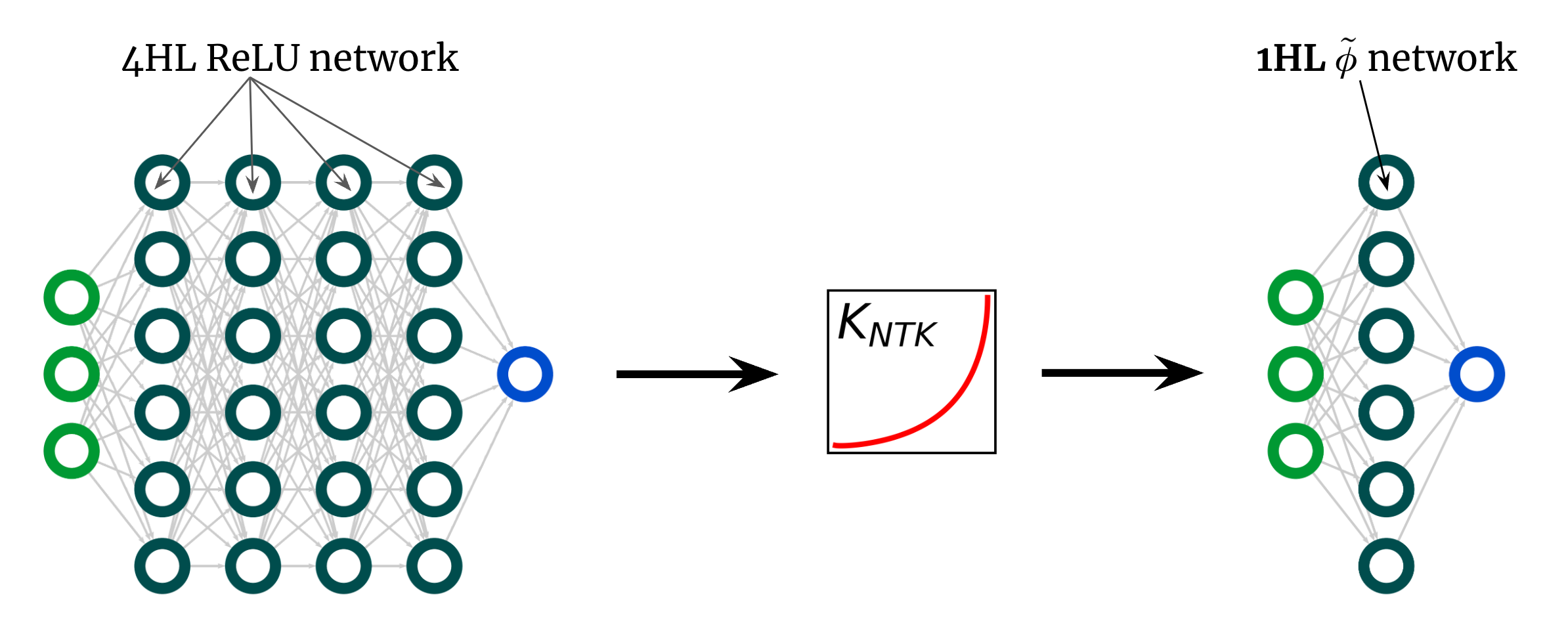
figue. 3. Surface $ReLUFCN à 1HL FCN avec fonction d’activation géométrique \tilde{\phi }.
Étonnamment, ces “superficiels” fonctionnent réellement. La sous-parcelle de gauche de la Fig. 4 ci-dessous montre une fonction d’activation \(\tilde {\phi }\) “simulée” qui donne en fait le même NTK que la profondeur FCN \(\textrm{ReLU}\). Les tracés de droite montrent ensuite le train + la perte de test + les traces de précision de trois FCN dans un problème tabulaire standard de l’ensemble de données UCI. Notez que bien que les réseaux ReLU peu profonds et profonds aient des comportements très différents, le réseau peu profond de simulation d’ingénierie suit le réseau profond presque exactement de la même manière !
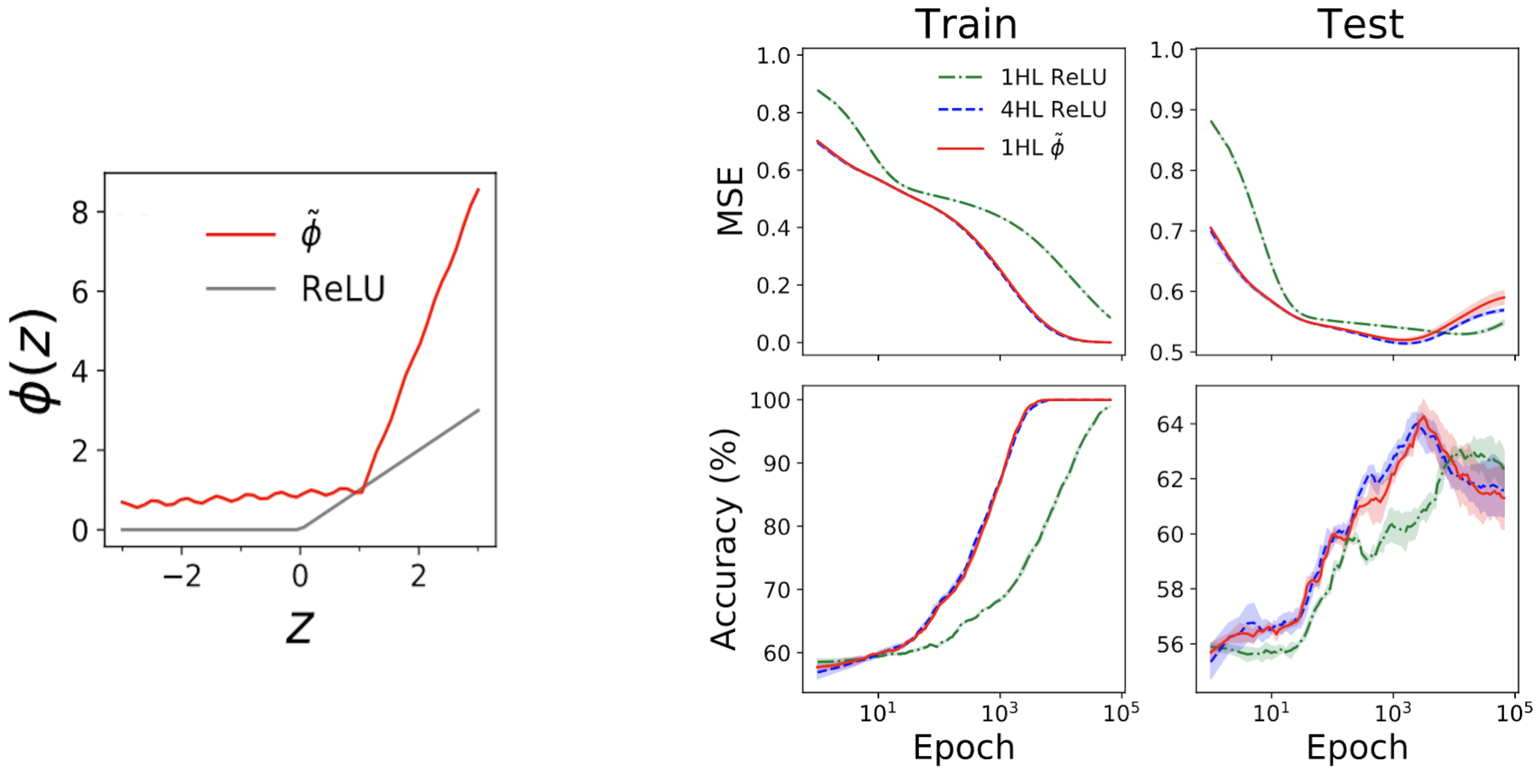
Figure 4. Panneau de gauche : fonction d’activation “simulée” conçue, tracée à l’aide de ReLU à des fins de comparaison. Panneaux de droite : les traces de performance de 1HL ReLU, 4HL ReLU et 1HL imitent les FCN formés sur l’ensemble de données UCI. Notez la correspondance étroite entre les réseaux d’imitation 4HL ReLU et 1HL.
Ceci est intéressant d’un point de vue technique, car un réseau peu profond utilise des paramètres inférieurs à un réseau profond pour obtenir les mêmes performances. Elle est également intéressante d’un point de vue théorique car elle soulève des questions fondamentales sur la valeur de la profondeur. Une croyance commune dans l’apprentissage en profondeur est que non seulement plus profond est plus profond, mais mieux Qualitativement différent: que les réseaux profonds apprendront efficacement des fonctions que les réseaux peu profonds ne peuvent tout simplement pas. Le résultat peu profond suggère que, du moins pour les FCN, ce n’est pas vrai : si nous savons ce que nous faisons, la profondeur ne nous achète rien.
Conclusion
Ce travail comporte de nombreuses mises en garde. Le plus important est que notre résultat ne s’applique qu’aux FCN, qui sont rarement récents. Cependant, les travaux sur les NTK convolutionnels progressent rapidement et nous pensons que ce modèle de conception de réseau par conception de noyau est mûr pour être étendu sous une forme ou une autre à ces architectures structurées.
Les travaux théoriques à ce jour ont fourni relativement peu d’outils pour les théoriciens pratiques de l’apprentissage en profondeur. Nous voulons que ce soit un modeste pas dans cette direction. Même sans que la science guide leur conception, les réseaux de neurones ont déjà permis des merveilles. Imaginez ce que nous pourrons en faire une fois que nous en aurons enfin un.
Cet article est basé sur l’article “Ingénierie inverse du noyau neuronal de l’ombre”, un travail conjoint avec Sajant Anand et Mike DeWeese. Nous fournissons un code pour reproduire tous nos résultats. Nous sommes heureux de répondre à vos questions ou commentaires.
