En apprentissage par renforcement coopératif multi-agents (MARL), parce que sur la politique On pense généralement que les méthodes de gradient de nature et de politique (PG) sont moins efficaces pour l’échantillonnage que les méthodes de décomposition de valeur (VD), qui sont hors de la politique. Cependant, certaines études expérimentales récentes montrent qu’avec une représentation d’entrée appropriée et un réglage des hyperparamètres, le PG multifactoriel peut atteindre des performances étonnamment robustes par rapport aux méthodes VD ex vivo.
Pourquoi les méthodes PG fonctionnent-elles si bien ? Dans cet article, nous présenterons une analyse concrète pour montrer que dans certains scénarios, par exemple, des environnements avec un paysage de récompense hautement multimodal, VD peut être problématique et conduire à des résultats indésirables. En revanche, les méthodes PG avec des politiques individuelles peuvent converger vers la politique optimale dans ces cas. De plus, les méthodes PG avec des politiques de régression automatique (AR) peuvent apprendre des politiques multimodales.
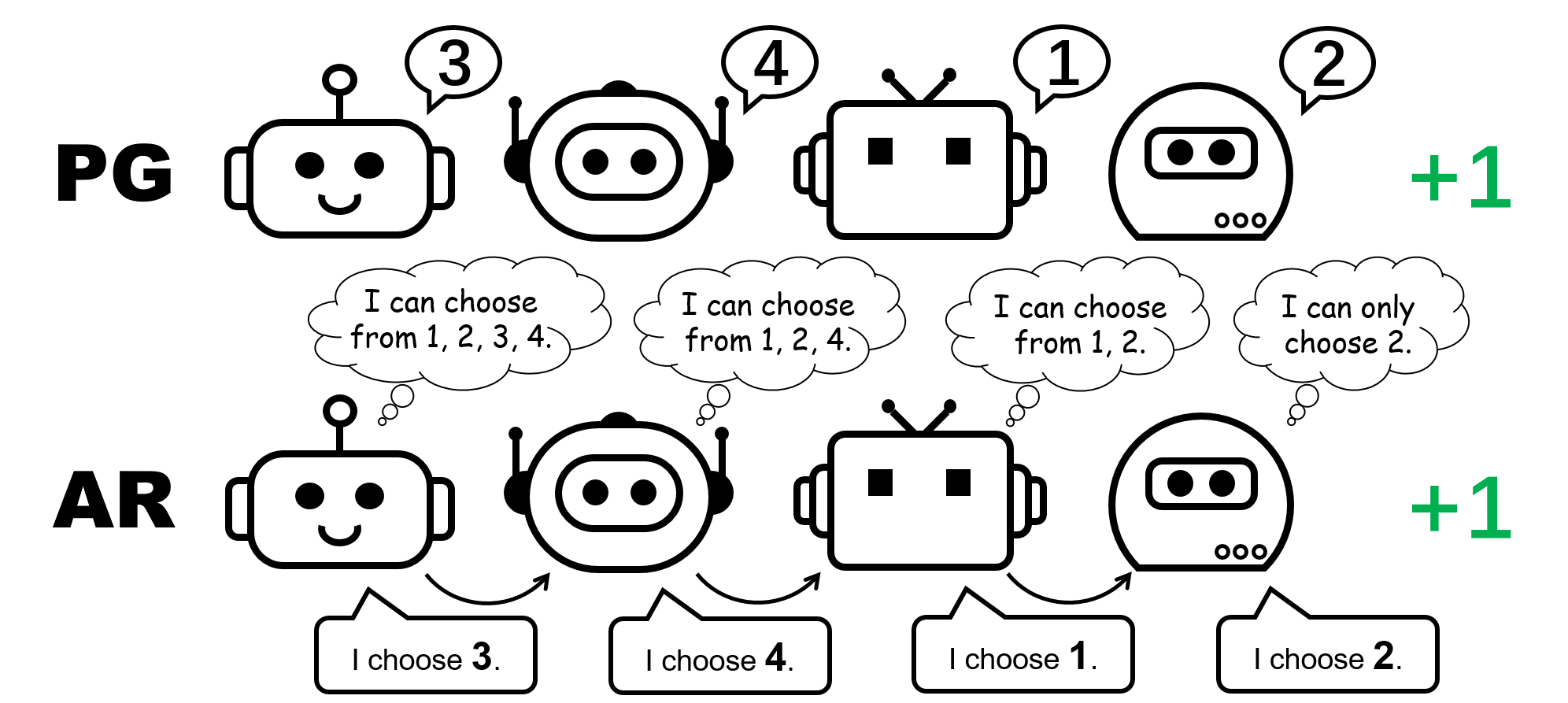
Figure 1 Différentes représentations politiques du jeu flip flop à 4 joueurs.
CTDE en MARL collaboratif : méthodes VD et PG
La formation centralisée et l’exécution décentralisée (CTDE) est un cadre commun dans la MARL collaborative. elle profite mondial Informations pour une formation plus efficace tout en conservant la représentation des politiques individuelles pour les tests. Le CTDE peut être mis en œuvre par l’analyse de la valeur (VD) ou le gradient politique (PG), ce qui conduit à deux types d’algorithmes différents.
Les méthodes VD apprennent les réseaux Q locaux et une fonction de mixage qui mélange les réseaux Q locaux avec une fonction Q globale. La fonction de mélange est généralement forcée de satisfaire le principe Individuel-Global-Max (IGM), qui garantit que la co-action optimale peut être calculée en sélectionnant avidement l’action localement optimale pour chaque agent.
En revanche, les méthodes PG appliquent directement le gradient de politique pour apprendre une politique individuelle et une fonction de valeur centrale pour chaque agent. La fonction de valeur prend comme entrée l’état global (par exemple, MAPPO) ou la séquence de toutes les observations locales (par exemple, MADDPG), pour une estimation précise de la valeur globale.
Flipping Game : Un contre-exemple simple où VD échoue
Nous commençons notre analyse en considérant un jeu coopératif sans état, le flipping game. Dans un jeu Switch à N joueurs, chaque agent peut produire N Actions {1,\ldots,N}. Les agents reçoivent une récompense de +1 si leurs actions sont mutuellement différentes, c’est-à-dire que l’action combinée est une permutation de plus de $1,\ldots,N$ ; Sinon, ils reçoivent un bonus de 0 $. Notez qu’il existe $N stratégies parfaites symétriques ! $ dans ce jeu.
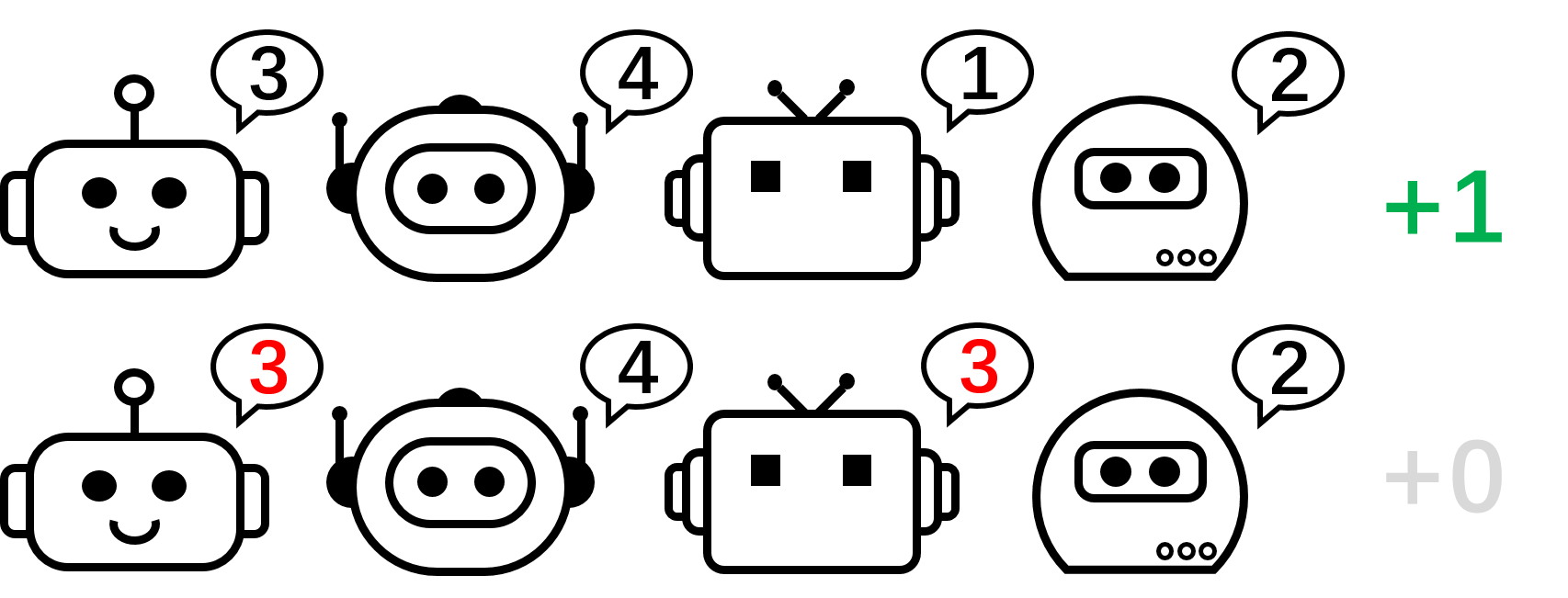
Figure 2 : Un jeu de switch à quatre joueurs.
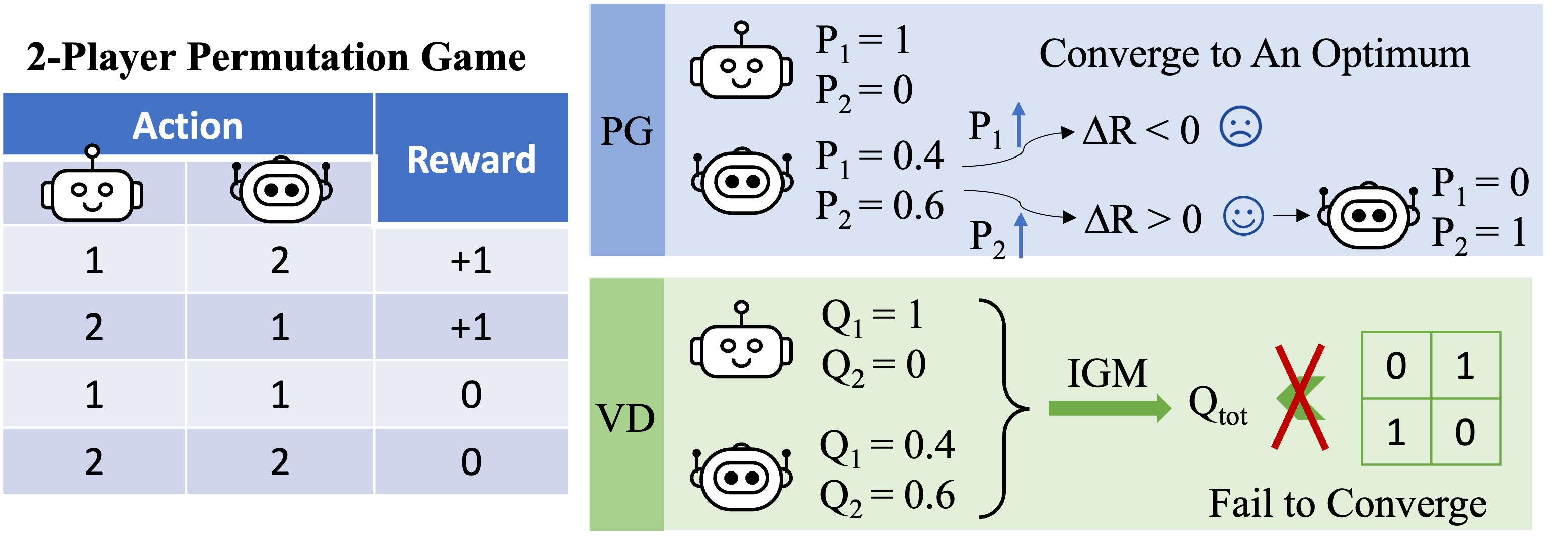
Figure 3 Une intuition de haut niveau sur la raison pour laquelle VD échoue dans le jeu de flop à deux joueurs.
Concentrons-nous maintenant sur le jeu de flop à deux joueurs et appliquons VD au jeu. Dans cette configuration sans état, nous utilisons Q1 et Q2 pour désigner les fonctions Q locales, et nous utilisons Qtot pour désigner la fonction Q globale. Le principe IGM l’exige
\(\arg \max_{a^1,a^2}Q_\textrm{tot}(a^1,a^2)=\{\arg \max_{a^1} Q_1(a^1),\ arg\max_{a^2}Q_2(a^2)\}.\)
Nous prouvons que VD ne peut pas représenter le gain du jeu de flop pour deux joueurs au moyen d’incohérences. Si les méthodes VD pouvaient représenter le gain, nous aurions
\(Q_\textrm{tot}(1,2)=Q_\textrm{tot}(2,1)=1\quad\text{and}\quad Q_\textrm{tot}(1,1)=Q_\ textrm {tot} (2,2) = 0.\)
Si l’un ou l’autre de ces deux mandataires a des valeurs Q locales différentes (disons Q1(1) > Q1(2), nous avons ∼arg≈a1Q1(a1)=1. Alors selon le principe IGM, n’importe quel coopération optimale
\((a^{1\étoile},a^{2\étoile})=\arg \max_{a^1,a^2} Q_\textrm{tot}(a^1,a^2)=\ {\arg \max_{a^1} Q_1(a^1), \arg \max_{a^2} Q_2(a^2)\}\)
satisfait a1étoile=1 et a1étoile}2, donc l’action combinée (a1,a2)=(2,1) est une sous- Optimisation est, par exemple, Q_\textrm{tot}(2,1)<1.
Sinon, si Q1(1)=Q1(2) et Q2(1)=Q2(2), alors
\(Q_\textrm{tot}(1, 1) = Q_\textrm{tot}(2,2) = Q_\textrm{tot}(1, 2) = Q_\textrm{tot}(2,1). \)
Par conséquent, l’analyse de la valeur ne peut pas représenter la matrice de récompense du jeu flop à deux joueurs.
Qu’en est-il des méthodes PG ? Les politiques individuelles peuvent en effet constituer une politique parfaite pour un jeu de flop. De plus, la descente de gradient aléatoire peut garantir que le PG converge vers l’une de ces options optimales sous des hypothèses modérées. Cela indique que bien que les méthodes PG soient moins courantes dans MARL que les méthodes VD, elles peuvent être préférées dans certains cas courants dans les applications du monde réel, par exemple, les jeux avec plusieurs modes de stratégie.
On remarque aussi que dans le jeu de permutation, pour représenter une politique commune idéale, chaque agent doit choisir des actions distinctes. Ainsi, une mise en œuvre réussie de PG doit garantir que les politiques sont spécifiques au proxy. Cela peut être fait en utilisant des politiques uniques avec des paramètres non partagés (appelées PG-Ind dans notre article), ou une politique conditionnelle à l’ID proxy (PG-ID).
PG surpasse les méthodes VD existantes dans les salles d’examen MARL populaires
Au-delà de la simple illustration d’un jeu de retournement, nous avons étendu notre étude à des critères MARL communs et plus réalistes. En plus du StarCraft Multi-Agent Challenge (SMAC), où l’efficacité du PG a été validée et la politique adaptée à l’agent introduite, nous affichons de nouveaux résultats dans Google Research Football (GRF) et le Hanabi Multiplayer Challenge.
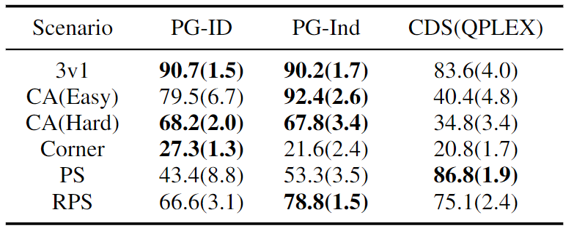
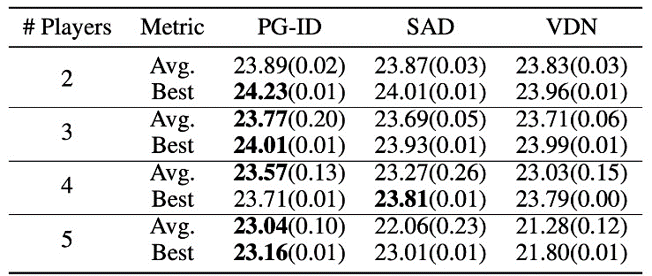
Figure 4 Taux de réussite (à gauche) des méthodes PG sur GRF ; (À droite) Les meilleures et moyennes notes sur Hanabi-Full.
Dans GRF, les méthodes PG surpassent les dernières lignes de base VD (CDS) dans 5 scénarios. Fait intéressant, nous notons également que les politiques uniques (PG-Ind) sans paramètres de partage atteignent des taux de réussite similaires, et parfois plus élevés, que les politiques spécifiques au proxy (PG-ID) dans les cinq scénarios. Nous évaluons PG-ID dans un jeu Hanabi à grande échelle avec un nombre variable de joueurs (2 à 5 joueurs) et le comparons avec SAD, une variante robuste de l’apprentissage Q par extrapolation Hanabi, et des réseaux d’analyse de valeur (VDN). Comme indiqué dans le tableau ci-dessus, PG-ID est capable d’obtenir des résultats similaires ou meilleurs que les meilleures récompenses moyennes obtenues par SAD et VDN avec un nombre variable de joueurs utilisant le même nombre d’étapes d’environnement.
Au-delà des récompenses plus élevées : apprentissage du comportement multimodal grâce à la modélisation automatique des politiques de régression
En plus d’apprendre des récompenses plus élevées, nous examinons également comment les politiques multimodales sont apprises dans la MARL collaborative. Revenons au jeu de retournement. Bien que nous ayons démontré que PG peut apprendre efficacement la politique optimale, le mode de stratégie qu’il atteint finalement peut dépendre grandement de l’initialisation de la politique. Ainsi, la question naturelle serait :
Pouvons-nous apprendre une politique unique qui puisse couvrir toutes les situations optimales ?
Dans une formulation PG décentralisée, la représentation globale d’une politique partagée ne peut représenter qu’un modèle particulier. Par conséquent, nous proposons une méthode améliorée de paramétrage des politiques pour une expression plus forte : les politiques de régression automatique (AR).

Figure 5 Comparaison des politiques individuelles (PG) et des politiques de régression automatique (AR) dans un jeu de flop à quatre joueurs.
Formellement, nous compilons la politique partagée de n $ agents sous la forme de
\(\pi (\mathbf{a}\mid \mathbf{o})\presque \prod_{i=1}^n\pi _{\theta ^{i}}\left(a^{i}\mid o ^{i},a^{1},\ldots,a^{i-1} \right),\)
où l’action produite par l’agent i dépend de sa propre observation oi et de toutes les actions des agents précédents 1,dots,i-1. Il peut représenter l’opérateur de régression automatique n’importe quel Une politique commune dans le programme de développement municipal central. le Juste La modification de la politique de chaque agent est la dimension d’entrée, qui est légèrement élargie en incluant les actions précédentes ; La dimension de sortie de chaque politique de procuration reste inchangée.
Avec une telle surcharge de paramètres minimale, la politique AR améliore considérablement la puissance de représentation des méthodes PG. Nous notons que PG avec politique AR (PG-AR) peut représenter simultanément tous les modes de politique optimaux dans le jeu de retournement.

Figure : PG-Ind (à gauche) et PG-AR (au milieu) cartes thermiques des actions politiques apprises et carte thermique des récompenses (à droite) ; Alors que PG-Ind ne converge que sur un mode spécifique dans un jeu de flop à 4 joueurs, PG-AR détecte avec succès tous les modes optimaux.
Dans des environnements plus complexes, y compris SMAC et GRF, PG-AR peut apprendre des comportements émergents intéressants qui nécessitent une forte coordination au sein de l’agent que PG-Ind peut ne jamais apprendre.
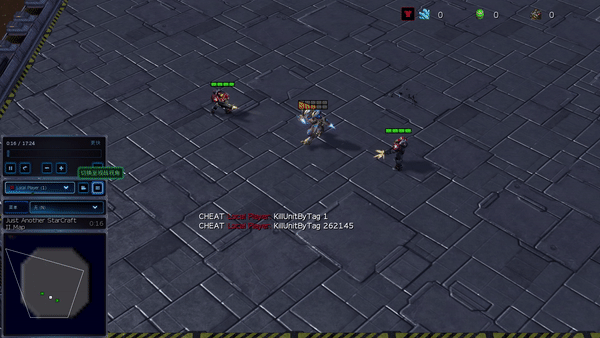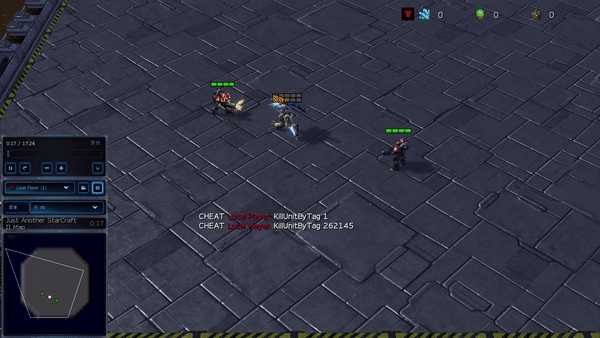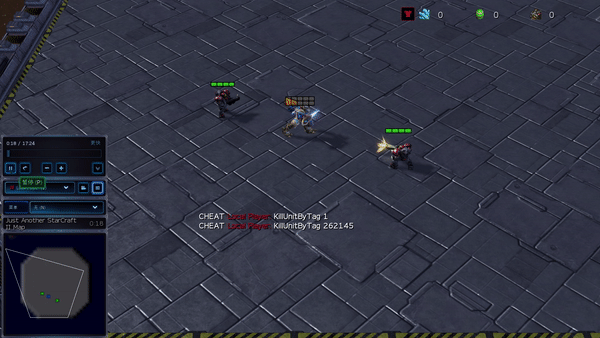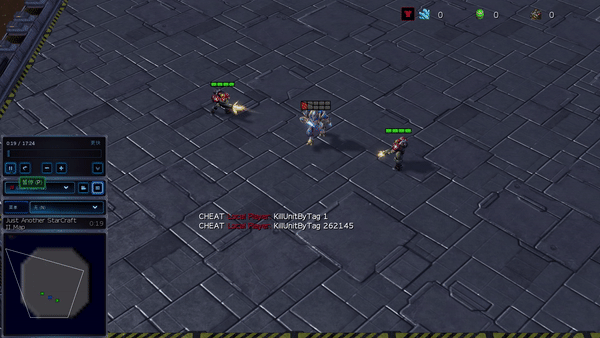
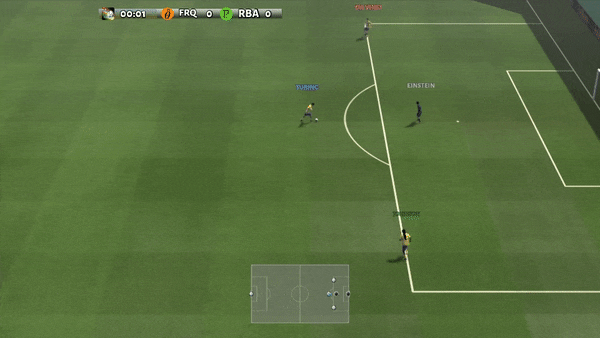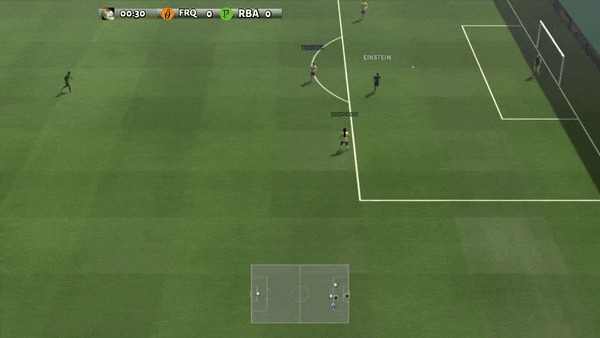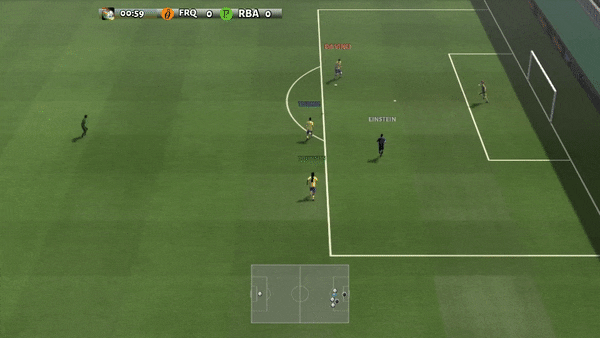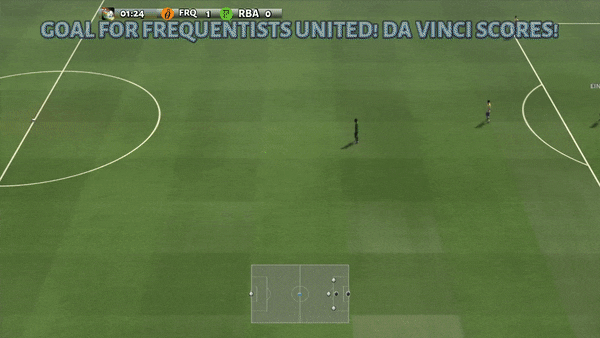
Figure 6 (à gauche) Comportement émergent induit par PG-AR dans SMAC et GRF. Sur la carte 2m_vs_1z de SMAC, les Marines continuent de se tenir debout et d’attaquer à tour de rôle en s’assurant qu’un seul Marine à la fois ; (À droite) Dans le scénario Academy_3_vs_1_with_keeper GRF, les agents apprennent un comportement de style « Tiki-Taka » : chaque joueur continue de passer le ballon à ses coéquipiers.
Discussions et plats à emporter
Dans cet article, nous présentons une analyse concrète des méthodes VD et PG en MARL collaborative. Tout d’abord, nous révélons les limites de l’expression des modes VD communs, montrant qu’ils ne peuvent pas représenter des politiques optimales même dans un simple jeu de permutation. En revanche, nous montrons que les méthodes PG sont manifestement plus expressives. Nous étudions expérimentalement l’avantage expressif du PG dans les tests MARL populaires, y compris le SMAC, le GRF et le Hanabi Challenge. Nous espérons que les enseignements tirés de ce travail bénéficieront à la communauté vers des algorithmes MARL collaboratifs plus généraux et plus robustes à l’avenir.
Cet article est basé sur notre article : Revisiting Some Common Practices in Multifactor Cooperative Reinforcement Learning (article, site web).
